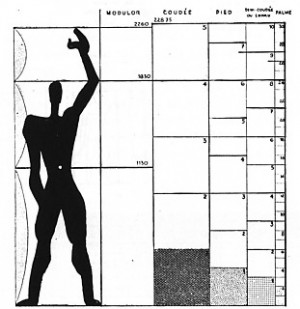
モデュロールとは規格化
本書は建築に新たな規格をもたらそうとする野心的な本だ。新たな規格とは「人が手をあげた状態での高さ」と、その身長を基準とする。
手をあげた高さを二等分した辺をもつ正方形を二つ並べ、対角線を引き、その対角線を半径とする円弧を描き、正方形の辺を伸ばした線と円弧とが交わる点同士を結び直角三角形を描く、さらにその三角形の長辺を二等分して・・・というように幾何学的な操作をしながら、それぞれの線の長さと比率の数字を列挙していく。
計算自体はそこまで難解なものではないが細かい数字が多数出てきて、その比率や長さが執拗に説明される。それが実際の建築にどのように生かされたかは、簡単な説明しかなされない。ここの長さとここの長さの比率をこの数字にした、と説明するときに、そこで用いられる数字に根拠を与えようとしているのが本書におけるコルビュジエの姿勢だ。
基準となるのは人体のサイズ
ここでコルビュジエがやろうとしているのは、『建築をめざして』で書かれた量産家屋の実践とも言える。単純に、まったく同じ住宅を複数建設するということだけではない。建てられる敷地の広さ、方角による採光具合、周辺の道のつくられかたなどの条件に合わせて変更可能な、それでいて規格化された住宅の設計である。重要なのは長さの「比率」であるので、同じ比率を使えば面積が広くなっても拡張することが可能なのだ。それは単純にサイズを大きくするということではなく、比率からもとめられる長さで空間を分割するということである。つまり、四分割するとき、五分割するときなど、組み合わせが変わっても同じ規格を使用していれば新たに一から設計する必要はないのである。
これはちょうど日本の住宅における畳と同じだ。畳の枚数で四畳半、六畳、八畳というふうに部屋のレイアウトと部屋数を調整するときの作業に近い。畳はその縦と横の長さが同じである。コルビュジエが本書でおこなおうとしていることも、畳の縦横の規格にあたるものをつくろうとしていると言えるだろう。
コルビュジエは次のように語る。
「パルテノンも、インドの寺院も、教会堂も、正確な尺度で建築された」
「一定の規則に従い連絡ある系統をなし、根本的な統一をさえ認めているところの尺度である」
「いかなる道具を用いたのであろうか?それは永久にかわることのない道具、しかも貴い道具であった。」
「単刀直入にいうならば、人体各部の寸法から出発したものなのである。」

パルテノン神殿(wikimedia.orgより)
人体の各部位はサイズを計測する道具でもあった。たとえば、親指と人差し指の幅いくつ分か、手の中指から肘までの長さがいくつ入る長さか、ひとまたぎした長さ何歩分か、というように。それは「現代においても人間の道具なのである」とコルビュジエはいう。
人体から導き出される数字
最初コルビュジエは身長175cm、手をあげた高さ216cmという数字を使っている。途中の計算の説明では手をあげた高さを220cmとして、その半分の110cmの正方形を二つ並べる操作に使用している。さらに別の箇所では、手をあげたときの226cm、身長183cmで書き進められていく。
これらの数字は本書を読みすすめていくと、あたかもマジックナンバーのように使われれる。たとえば歴史的な建築物である、何々の壁を計測してみたら同じ数字だった、どこそこはその半分の数字だった、というふうに。コルビュジエはこの時期メジャーを携帯し、行く先々でさまざまな部分の長さを測っていたという。
建てはじめたら簡単には修正がきかないからこそ
建築において数字は重要なものであるのは間違いない。たとえば天井までの高さをどれくらいにするか、入口のドアの高さをどうするか、階段の高さと幅、廊下の幅、部屋の壁の長さ、窓の大きさなど、すべては設計時点に数字で決められる。
人間の目が美しいと感じる比率として黄金比というものが存在する。黄金比を元に美しさを規格化しようとすれば不可能ではないのかもしれない。建築において、視覚的な美しさや利用者の使いやすさを考慮したとき、人体のサイズをもとに規格化するのは理に適った方法だ。
設計時点で決める数値、その根拠を必要とするとき、基準となるのは人体のサイズなのだ。この規格を用いて設計すれば、狭すぎる廊下や低すぎる階段、意味のない高さを持った天井などという「間違った」設計は回避できるはずだ。

シトロエン住居(http://www.fondationlecorbusier.frより)
しかし、コルビュジエが考えてるのはこのような単純なことだけではない。単に「間違った」設計をしないために基準の数字を用いるのではなく、「美しい」設計を可能にするためにその幾何学で裏打ちされた黄金の数字を用いようとする。それがモデュローである。建築家の芸術的なセンスに頼らずに数学的に計算された、つまり誰にでも利用可能な数字だ。このモデュロールによって量産されるのは建築そのものではなく、建築家あるいは芸術家であるとも言える。
芸術は数学的に解釈可能か
芸術家、建築家の作品を数学的に制作するということが果たして可能なのだろうか? それに対する回答はコルビュジエ自身が本書のなかで書いている。
「どんな道具でもどんな公式でも、私の自由を奪うようなものであるならば、私はそれと闘うだろう。私は自由をほんとに無傷で保ちたいのだ。黄金数やある線が完全な正統的な解答をもたらしてくれようとも、私は「それはあるいは正しいかも知れないが、美しくない」と文句をいうだろう。」
つまりここでは数学的な作業を否定している。数字ではなく、あくまでも自分が美しいと思えることが重要だと言うのだ。コルビュジエ自身、モデュロールのもつ「矛盾」について気づいている。すなわち、規格化の重要性と芸術家の美に対する感覚とのあいだに生じる矛盾である。

サヴォア邸
(http://crownarchitect.blog121.fc2.com/より)
モデュロールの反響
コルビュジエは 『モデュロールⅠ』、『モデュロールⅡ』の二冊の書籍を書いている。
日本では1970年代半ばの同時期に翻訳されて刊行されているが、本国では『Ⅰ』が1948年、『Ⅱ』がその6年後の1954年に出版されている。『Ⅰ』ではモデュロールの内容についての説明がなされ、『Ⅱ』ではそれに対する反響を中心にまとめられている。
反響のなかには、じつは『モデュロールⅠ』でおこなっているコルビュジエの計算が数学的に誤りであるという指摘が少なくない。ミュンヘンの学生からおくられたその指摘についての記述でコルビュジエは応える、この学生の指摘は「正確だが美しくない」と。
また、アンリ・カーンワイラーからの手紙も紹介される。アンリ・カーンワイラーは当時、パリで活動していた画商であり、美術評論家でもある。ピカソやブラックの作品を多く扱い、キュビズム運動を影で支えたとも言える重要な人物である。

Villa de Madame H. de Mandrot
(http://www.fondationlecorbusier.fr)
カーンワイラーは、基本的にはモデュロールの考えを採用するのは正しいとする。それによって「無政府状態からのれる」ことができると考えている。しかし、このモデュロールによって美がつくられると信じることはできないという。
「美しさとは幾人かの―大芸術家―に与えられた神秘的な才能で、これを作品に付与するものであります」
つまり数字を合わせることで誰にでも生み出せるものではないということだ。
本書の前半に流れる勢いのある考察は後半でやや大人しくなる。モデュロールに基づいて設計されたコルビュジエの作品は少なくない。後半では実際の運用について書かれている。とはいえこのモデュロールはその後、建築界に根付くような”規格”とはならなかった。ある種の美しさには規則があるかもしれない。しかし規則があればそこに必ず美しさがあるわけでない。